Comparison Geometry 2019

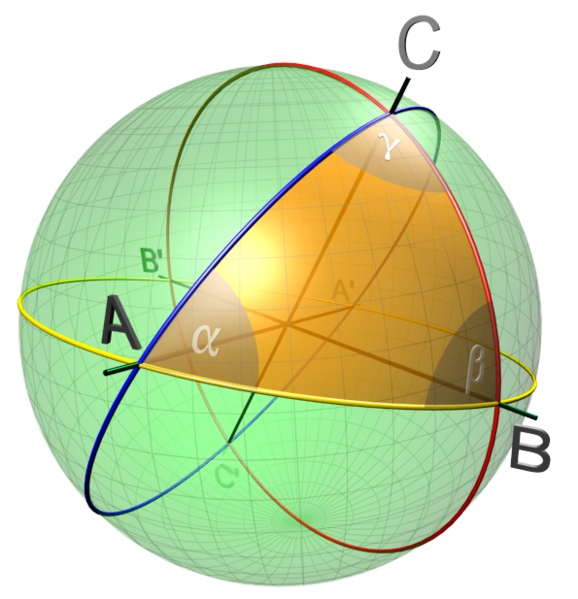
General Remarks: The basic idea of comparison geometry is to compare the geometry of an arbitrary Riemannian manifold M with the geometry of constant curvature spaces (flat space, the spheres and hyperbolic spaces) to obtain information on the properties of M. To give a vivid description recall that triangles on a sphere are fatter than triangles in flat space and that the sum of interior angles of a spherical triangle generally exceeds Pi. A typical statement in comparison geometry would now be that if M has (sectional) curvature bounded below by some k>0 then the triangles of M are fatter than those of M_k, the sphere of curvature k. The theory that is bulit upon such and similar ideas has lead to a wealth of important results that firmly belong to the standard tool-kit of Riemannian geometry. In particular, this includes some of the most important theorems, which allow to obtain global information on the geometry and topology of Riemannian manifolds.

Contents and prerequsites: This course provides an introduction to comparison geometry maninly of Riemannian manifolds with some excursions into the semi-Riemannian/Lorentzian realm. We present the main results and discuss the main techniques of the theory assuming basic knowledge in Riemannian geometry (as provided by a typical standard course, see e.g. our lecture notes) and of course basic konwledge of differential geometry (again as provided by a typical first course, see e.g. the lecture notes of Mike Kunzinger). In addidtion we will use some basics on covering spaces and also some ODE-theory.

We will, however, start the course by discussing some fundamentals of Riemannian geometry (to also allow students from different curricula as e.g. theoretical physics to enter the course) such as geodesics, the exponential map, geodesic variations and Jacobi fields. As a first result we will prove Myers' theorem which states that a (complete, conected) Riemannian manifold with Ricci-curvature bounded below by a positive constant is compact with an explicit bound on its diameter and a finite fundamental group. A further fundamental result we will present is the Rauch comparison theorem, which relates the sectional curvature to the rate at which geodesics spread apart. Finally we will prove Toponogov's triangle comparison theorem which is a precise version of the idea mentined above.

Target audience are primarily students in the mathematics master programme (specialising in geometry and topology) but also ambitious students in the theoretical physics master programme.

Position in the curriculum: Master Mathematics, compulsary module "Electives in Geometry" code MGEV. This course is also part of the Vienna Master Class Mathematical Physics.

Literature, reading list: This course is strongly influenced by Stefan Haller's lecture notes Differential Geometry III and a previous lecture course by Michael Kunzinger. Further standard sources are:

• Jost, Riemannian Geometry and Geometric Analysis
• Klingenberg, Riemannian Geometry
• O'Neill, Semi-Riemannian Geometry
• Petersen, Riemannian Geometry For the semi-Riemannian/Lorentzian case I will primarily use the Diploma thesis of Jan-Hendrik Treude.
  
  Exams will exclusively be oral on individual appointment starting end of Jannuary. Further information will be provided in due time.
  
  The language of instruction will be English unless all participants are sufficiently fluent in German.