Classification of two-body Heisenberg-like models due to the admitted ground statesAbstract
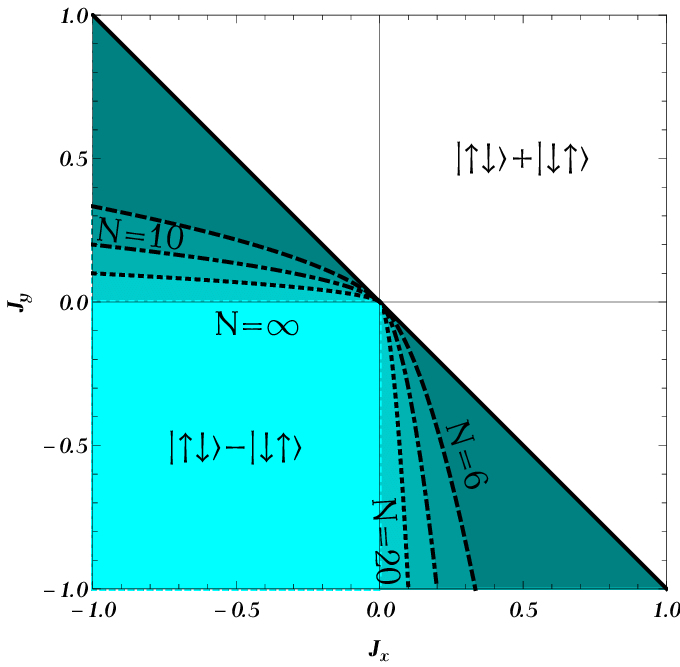
Frustration of classical many-body systems can be used to distinguish ferromagnetic interactions from anti-ferromagnetic ones via the Toulouse conditions. A quantum version of the Toulouse conditions provides a similar classification based on the local ground states. We compute the global ground states for a family of models with Heisenberg-like interactions and analyse their behaviour with respect to frustration, entanglement and degeneracy. For that we develop analytical and numerical analysing tools capable of quantifying the interplay between those three quantities. We find that the quantum Toulouse conditions provide a proper classification, however, refinements can be found. Our results show how the different local ground states affect the interplay and pave the way for further generalisation and possible applications to other quantum many-body systems.