Spontaneous collapse: A solution to the measurement problem and a source of the decay in mesonic systems

Abstract

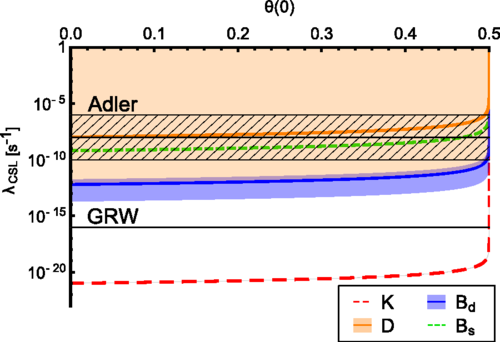
Dynamical reduction models propose a solution to the measurement problem in quantum mechanics: the collapse of the wave function becomes a physical process. We compute the predictions to decaying and flavor-oscillating neutral mesons for the two most promising collapse models, the QMUPL (quantum mechanics with universal position localization) model and the mass-proportional CSL (continuous spontaneous localization) model. Our results are showing (i) a strong sensitivity to the very assumptions of the noise field underlying those two collapse models and (ii) under particular assumptions the CSL case allows one even to recover the decay dynamics. This in turn allows one to predict the effective collapse rates solely based on the measured values for the oscillation (mass differences) and the measured values of the decay constants. The four types of neutral mesons (K meson, D meson, Bd meson, and Bs meson) lead surprisingly to ranges comparable to those put forward by Adler [J. Phys. A: Math. Theor. 40, 2935 (2007)] and Ghirardi, Rimini, and Weber [Phys. Rev. D 34, 470 (1986)]. Our results show that these systems at high energies are very sensitive to possible modifications of the standard quantum theory, making them a very powerful laboratory to rule out certain collapse scenarios and study the detailed physical processes solving the measurement problem.