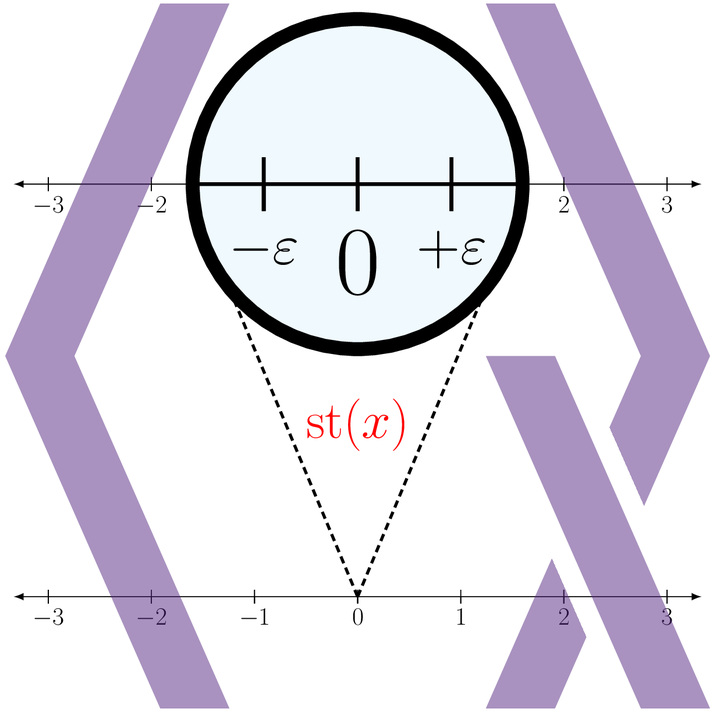
 Representation of the hyperreal line
Representation of the hyperreal lineAbstract
Non-Archimedean mathematics is an approach based on fields which contain infinitesimal and infinite elements. Within this approach, we construct a space of a particular class of generalized functions, ultrafunctions. The space of ultrafunctions can be used as a richer framework for a description of a physical system in quantum mechanics. In this paper, we provide a discussion of the space of ultrafunctions and its advantages in the applications of quantum mechanics, particularly for the Schrödinger equation for a Hamiltonian with the delta function potential.
Type
Publication
In Quantum