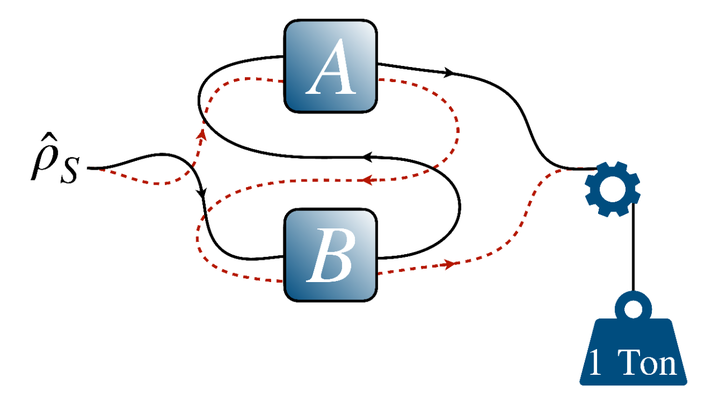
Ergotropic work is extracted from a system that undergoes the consecutive action of two channelsAbstract
We characterize the impact that the application of two maps in a quantum-controlled order has on the process of work extraction via unitary cycles and its optimization. The control is based on the quantum switch model that applies maps in an order not necessarily compatible with the underlying causal structure and, in principle, can be implemented experimentally. First, we show that the activation of quantum maps through the quantum switch model always entails a non-negative gain in ergotropy compared to their consecutive application. We also establish a condition that the maps should fulfill in order to achieve a nonzero ergotropic gain. We then perform a thorough analysis of maps applied to a two-level system and provide general conditions for achieving a positive gain on the incoherent part of ergotropy. Our results are illustrated with several examples and applied to qubit and d-dimensional quantum systems. In particular, we demonstrate that a nonzero work can be extracted from a system thermalized by two coherently controlled reservoirs.