Euler Characteristics

When you take a polyhedron and count its faces F, edges E and vertices V, and compute

χ = F - E + V

then you always find the same answer. This χ is called the Euler characteristic. Try it with the five Platonic solids.

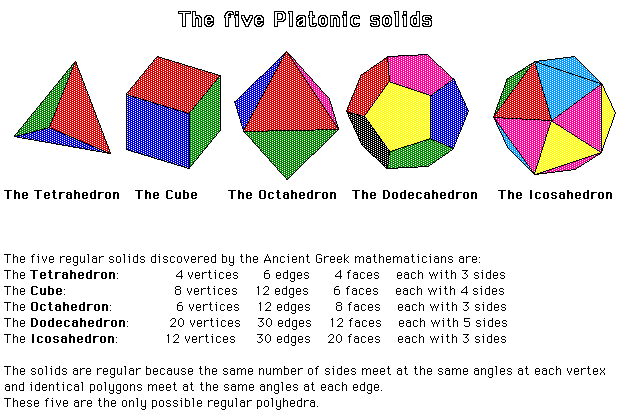
For each of the five Platonic solids we find χ = F - E + V = 2. This is a theorem:

Theorem: Every polyhedron has Euler characteristic χ = 2.

Euler, who came up with this in 1758, was in fact surprised that no one before him noticed this relation. We won't give the proof here, but it can be found in many topology books, e.g.

• Edwin Spanier: Algebraic Topology, Springer 1966, p. 205.
• Wikepedia gives the proof: here. It was actually Cauchy who gave the first rigorous proof of this theorem. Euler didn't care about rigour too much.
• I. Lakatos, Proofs and Refutations, Cambridge University Press, 1976, ISBN 0 521 29038 4

Try it with a football, or the 'golfball' on the campus of the University of Surrey, or the star on the right.

I don't remember how many faces a standard football has, but it has only pentagons and hexagons. Let's try to compute how many there are, using the Euler characteristic. Assume that there are are a pentagons and b hexagons. Verify the following equation:

F = a + b
E = (5a + 6b)/2	(divide by two in order not to double count edges)
V = (5a + 6b)/3	(divide by three in order not to triple count vertices)
F - E + V = 2

Since E and V are integers, a must be a multiple of 6, say a = 6k. Then we get.

F = 6k + b

E = (5 * 6k + 6b)/2 = 15k + 3b

E = (5 * 6k + 6b)/3 = 10k + 2b

F - E + V = 2 = (6k + b) - (15k + 3b) + (10k + 2b) = k

Therefore k = 2, so there are always 2*6 = 12 pentagons. But I still don't know how many hexagons.

Questions:	1: Is there a 'football' with no hexagons at all? Solution
	2: Every bee knows that one can tile the plane with only hexagons. Can one tile the earth with only hexagons? Solution
	3: The `golfball' has 528 triangles, 18 quadrilaterals and 1 base of 24 sides. Compute F, E and V. Solution

The book of Lakatos is about the philosophy of science, and not so much about mathematics. On of its aims is to explain how the notions and definitions in science (including mathematics) are developed rather than stated correctly once and for all. It's about a maths class discussing the Euler characteristic and the proof of the above theorem, and shows how the understanding of polyhedra (but one can take any other notion in science just as well) evolves as the students try to grasp the proof that the teacher presents. It is actually pretty hard to define what a polyhedron really is. For example, are the figures below polyhedra. What are their Euler characteristics?

It turns out, closed surfaces are topologically different if they have different Euler characteristics. (By closed surface, we mean a surface without boundary.) The torus has Euler characteristic 0, the pretzel (a torus with two holes) has Euler characteristic -2, and every hole that you add reduces the Euler characteristic by 2. There are also non-orientable closed surfaces; a famous one is the Klein bottle; it has Euler characteristic 0.

torus: χ = 0	'pretzel': χ = -2	Klein bottle: χ = 0	Projective plane: χ = ?

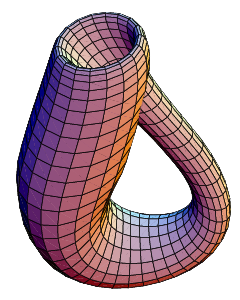
I am talking now about surfaces, not about polyhedra any more. But you can compute the Euler characteristic of a surface by simply drawing a polyhedron on it (just like drawing the faces on a football), and count the faces, edges and vertices. If the surface is not a sphere, then you need to make sure that the faces are simple polygons, and not cylindrical or Möbius bands or even more complicated things. Non-spherical surfaces have Euler characteristics different from 2!

Let me say a few words about orientable and non-orientable surfaces. A non-orientable surface does not have a proper inside or outside. The best known example is the Möbius band. If you put a non-symmetric figure on it, for example the letter R, and slide it over an appropriate loop, then it returns to the original position in mirror image. The Möbius band has a boundary. This boundary can be is sewn up (in two different ways) to produce non-orientable surfaces (the Klein bottle and the projective plane) without boundary.

Escher's Möbius band. Never mind the ants, but they are all walking on the same side of the Möbius band, because it has only one side. (For more info on Möbius bands, see e.g. the

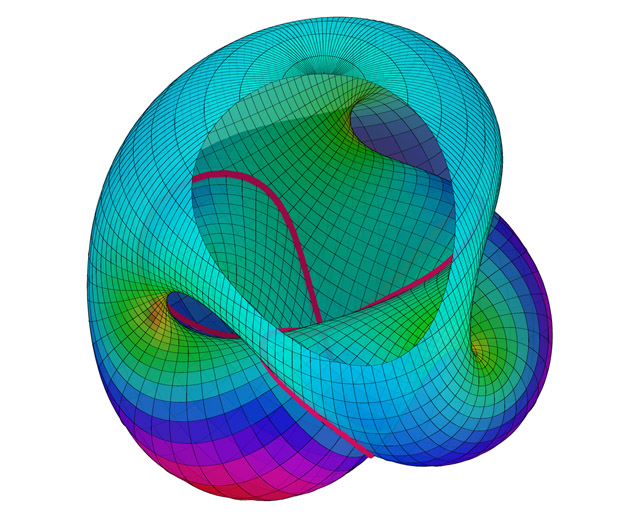
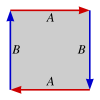
Back to the Euler characteristic. It may be difficult to draw a polyhedron on a surface as the Klein bottle, even if you happen to find one on the street. There is a trick for this. Draw a polygon and identify sides. With a torus it is not so difficult to imagine how this works. Think of a square sheet of rubber, and fold it into a cylinder. This means that you effectively identify two opposite sides of the square. Now fold the two ends of the cylinder together (identifying the two other opposite sides of the square) and you have a torus.
There are in fact two ways (or orientations) of glueing the circular edges of two cylinders together. One is by simply putting the cylinders next to each other; the other is by sliding the one cylinder into the other and sewing the edges (one of each cylinder) together. When you try to do the latter for the two circular edges of a single cylinder you run into a little placing problem. But supposing you can solve that, you will have a Klein bottle.

torus	Identify opposite sides of the octogon to get a 'pretzel'	Klein bottle	projective plane

Sides of the polygons are identified in the direction of the arrows to create surfaces without boundary.
A different way of seeing the torus and pretzel is as with a sphere with one and two "handles". The genus of a surface is the number of handles.

Surfaces with boundary can be seen as surfaces without boundaries with holes in it. For example, the disk is a phere with one hole and the cylinder is a sphere with two holes in it.

The general formula for surfaces with handles and holes and crosscaps:

χ = 2- 2# handels - # holes - # crosscaps